Portal:Mathematics

The Mathematics Portal

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Refresh with new selections below (purge)

Featured articles – load new batch

Featured articles are displayed here, which represent some of the best content on English Wikipedia.

$Image 1 Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300). In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC). It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)$

Image 1
Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, $21$ is the GCD of $252$ and $105$ (as $252 = 21 \times 12$ and $105 = 21 \times 5)$ , and the same number $21$ is also the GCD of $105$ and $252 - 105 = 147$ . Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, $21 = 5 \times 105 + (-2) \times 252$ ). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)
Image 2

Cantor, c. 1910

Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.

Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Konstantin Gutberlet [de; it] was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)
Image 3
The manipulations of the Rubik's Cube form the Rubik's Cube group.

In mathematics, a group is a set with a binary operation that satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.

Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called ⁠ $1$ ⁠ (these properties characterize the integers in a unique way). (Full article...)
Image 4

Hilary Putnam

The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
Image 5

Elementary algebra studies which values solve equations formed using arithmetical operations.

Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.

Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
Image 6

Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.

While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in 17th-century studies of probability and annuities. Actuaries in the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems; actuaries use this knowledge to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)
Image 7

Portrait by August Köhler, c. 1910, after 1627 original

Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
Image 8
Plots of logarithm functions, with three commonly used bases. The special points $log b b = 1$ are indicated by dotted lines, and all curves intersect in $log b 1 = 0$ .

In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of $1000$ to base $10$ is $3$ , because $1000$ is $10$ to the $3$ rd power: $1000 = 10 3 = 10 \times 10 \times 10$ . More generally, if $x = b y$ , then $y$ is the logarithm of $x$ to base $b$ , written $log b x$ , so $log 10 1000 = 3$ . As a single-variable function, the logarithm to base $b$ is the inverse of exponentiation with base $b$ .

The logarithm base $10$ is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number $e \approx 2.718$ as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base $2$ and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written $log x$ . (Full article...)
Image 9
High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.

By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
Image 10

Kaczynski after his arrest in 1996

Theodore John Kaczynski (/kəˈzɪnski/ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle and lone wolf terrorism campaign to further his political agenda.

Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored a roughly 35,000-word manifesto and social critique called Industrial Society and Its Future which opposes all forms of technology, rejects leftism and fascism, advocates primitivism, and ultimately suggests violent revolution. (Full article...)
Image 11
The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.

In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
$\sum _{n=1}^{m}n(-1)^{n-1}.$

The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
$1-2+3-4+\cdots ={\frac {1}{4}}.$ (Full article...)
Image 12
The weighing pans of this balance scale contain zero objects, divided into two equal groups.

In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if $y$ is even then $y + x$ has the same parity as $x$ —indeed, $0 + x$ and $x$ always have the same parity.

Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
Image 13
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever is
present, including matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.

Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)
Image 14
Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).

In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
Image 15
In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.

Thus hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)

More featured articles

edit

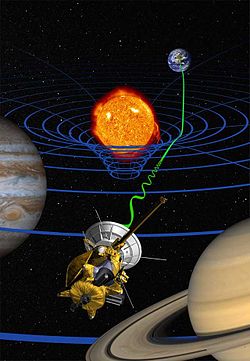
Selected image – show another

animation showing a roughly star-shaped graph being traced out as a smaller circle rolls around inside of a larger circle

Hypotrochoid

Credit: Sam Derbyshire

A hypotrochoid is a curve traced out by a point "attached" to a smaller circle rolling around inside a fixed larger circle. In this example, the hypotrochoid is the red curve that is traced out by the red point 5 units from the center of the black circle of radius 3 as it rolls around inside the blue circle of radius 5. A special case is a hypotrochoid with the inner circle exactly one-half the radius of the outer circle, resulting in an ellipse (see an animation showing this). Mathematical analysis of closely-related curves called hypocycloids lead to special Lie groups. Both hypotrochoids and epitrochoids (where the moving circle rolls around on the outside of the fixed circle) can be created using the Spirograph drawing toy. These curves have applications in the "real world" in epicyclic and hypocycloidal gearing, which were used in World War II in the construction of portable radar gear and may be used today in 3D printing.

More selected pictures

Good articles – load new batch

These are Good articles, which meet a core set of high editorial standards.

Image 1
Using the Pythagorean theorem to compute two-dimensional Euclidean distance

In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance.

These names come from the ancient Greek mathematicians Euclid and Pythagoras. In the Greek deductive geometry exemplified by Euclid's Elements, distances were not represented as numbers but line segments of the same length, which were considered "equal". The notion of distance is inherent in the compass tool used to draw a circle, whose points all have the same distance from a common center point. The connection from the Pythagorean theorem to distance calculation was not made until the 18th century. (Full article...)
Image 2

The graph of a function, drawn in black, and a tangent line to that graph, drawn in red. The slope of the tangent line is equal to the derivative of the function at the marked point.

In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation.

There are multiple different notations for differentiation. Leibniz notation, named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas prime notation is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leibniz notation by adding superscripts to the differentials, and in prime notation by adding additional prime marks. The higher order derivatives can be applied in physics; for example, while the first derivative of the position of a moving object with respect to time is the object's velocity, how the position changes as time advances, the second derivative is the object's acceleration, how the velocity changes as time advances. (Full article...)
Image 3
Donkey Kong Jr. Math is an edutainment platform video game developed and published by Nintendo for the Nintendo Entertainment System. It is a spin-off of the 1982 arcade game Donkey Kong Jr. In the game, players control Donkey Kong Jr. as he solves math problems set up by his father Donkey Kong. It was released in Japan in 1983 for the Family Computer, and in North America and the PAL region in 1986.

It is the only game in the Education Series of NES games in North America, owing to the game's lack of success. It was made available in various forms, including in the 2002 GameCube video game Animal Crossing and on the Virtual Console services for Wii and Wii U in 2007 and 2014 respectively, and in 2024 for the Nintendo Classics service. Donkey Kong Jr. Math was a critical and commercial failure. It has received criticism from several publications including IGN staff, who called it one of the worst Virtual Console games. (Full article...)
Image 4
Klaus Friedrich Roth (29 October 1925 – 10 November 2015) was a German-born British mathematician who won the Fields Medal for proving Roth's theorem on the Diophantine approximation of algebraic numbers. He was also a winner of the De Morgan Medal and the Sylvester Medal, and a Fellow of the Royal Society.

Roth moved to England as a child in 1933 to escape the Nazis, and was educated at the University of Cambridge and University College London, finishing his doctorate in 1950. He taught at University College London until 1966, when he took a chair at Imperial College London. He retired in 1988. (Full article...)
Image 5

Two symmetric orthographic projections

In geometry, the complete or final stellation of the icosahedron^[1] is the outermost stellation of the icosahedron, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram. That is, every three intersecting face planes of the icosahedral core intersect either on a vertex of this polyhedron or inside of it. It was studied by Max Brückner after the discovery of Kepler–Poinsot polyhedron. It can be viewed as an irregular, simple, and star polyhedron. (Full article...)
$Image 6 "The Gherkin", 30 St Mary Axe, London, completed 2003, is a parametrically designed solid of revolution. Mathematics and architecture are related, since architecture, like some other arts, uses mathematics for several reasons. Apart from the mathematics needed when engineering buildings, architects use geometry: to define the spatial form of a building; from the Pythagoreans of the sixth century BC onwards, to create architectural forms considered harmonious, and thus to lay out buildings and their surroundings according to mathematical, aesthetic and sometimes religious principles; to decorate buildings with mathematical objects such as tessellations; and to meet environmental goals, such as to minimise wind speeds around the bases of tall buildings. In ancient Egypt, ancient Greece, India, and the Islamic world, buildings including pyramids, temples, mosques, palaces and mausoleums were laid out with specific proportions for religious reasons. In Islamic architecture, geometric shapes and geometric tiling patterns are used to decorate buildings, both inside and outside. Some Hindu temples have a fractal-like structure where parts resemble the whole, conveying a message about the infinite in Hindu cosmology. In Chinese architecture, the tulou of Fujian province are circular, communal defensive structures. In the twenty-first century, mathematical ornamentation is again being used to cover public buildings. (Full article...)$

Image 6
"The Gherkin", 30 St Mary Axe, London, completed 2003, is a parametrically designed solid of revolution.

Mathematics and architecture are related, since architecture, like some other arts, uses mathematics for several reasons. Apart from the mathematics needed when engineering buildings, architects use geometry: to define the spatial form of a building; from the Pythagoreans of the sixth century BC onwards, to create architectural forms considered harmonious, and thus to lay out buildings and their surroundings according to mathematical, aesthetic and sometimes religious principles; to decorate buildings with mathematical objects such as tessellations; and to meet environmental goals, such as to minimise wind speeds around the bases of tall buildings.

In ancient Egypt, ancient Greece, India, and the Islamic world, buildings including pyramids, temples, mosques, palaces and mausoleums were laid out with specific proportions for religious reasons. In Islamic architecture, geometric shapes and geometric tiling patterns are used to decorate buildings, both inside and outside. Some Hindu temples have a fractal-like structure where parts resemble the whole, conveying a message about the infinite in Hindu cosmology. In Chinese architecture, the tulou of Fujian province are circular, communal defensive structures. In the twenty-first century, mathematical ornamentation is again being used to cover public buildings. (Full article...)
Image 7

Detail of Averroes in a 14th-century painting by Andrea di Bonaiuto

Ibn Rushd (14 April 1126 – 11 December 1198), archaically Latinized as Averroes, was an Andalusian Muslim polymath and jurist who wrote about many subjects, including philosophy, theology, medicine, astronomy, physics, psychology, mathematics, Islamic jurisprudence and law, and linguistics. The author of more than 100 books and treatises, his philosophical works include numerous commentaries on Aristotle, for which he was known in the Western world as The Commentator and Father of Rationalism.

Averroes was a strong proponent of Aristotelianism; he attempted to restore what he considered the original teachings of Aristotle and opposed the Neoplatonist tendencies of earlier Muslim thinkers, such as al-Farabi and Avicenna. He also defended the pursuit of philosophy against criticism by Ash'ari theologians such as Al-Ghazali. Averroes argued that philosophy was permissible in Islam and even compulsory among certain elites. He also argued scriptural text should be interpreted allegorically if it appeared to contradict conclusions reached by reason and philosophy. In Islamic jurisprudence, he wrote the Bidāyat al-Mujtahid on the differences between Islamic schools of law and the principles that caused their differences. In medicine, he proposed a new theory of stroke, described the signs and symptoms of Parkinson's disease for the first time, and might have been the first to identify the retina as the part of the eye responsible for sensing light. His medical book Al-Kulliyat fi al-Tibb, translated into Latin and known as the Colliget, became a textbook in Europe for centuries. (Full article...)
Image 8
In the mathematical fields of graph theory and finite model theory, the logic of graphs deals with formal specifications of graph properties using sentences of mathematical logic. There are several variations in the types of logical operation that can be used in these sentences. The first-order logic of graphs concerns sentences in which the variables and predicates concern individual vertices and edges of a graph, while monadic second-order graph logic allows quantification over sets of vertices or edges. Logics based on least fixed point operators allow more general predicates over tuples of vertices, but these predicates can only be constructed through fixed-point operators, restricting their power.

A sentence $S$ may be true for some graphs, and false for others; a graph $G$ is said to model $S$ , written $G\models S$ , if $S$ is true of the vertices and adjacency relation of $G$ . The algorithmic problem of model checking concerns testing whether a given graph models a given sentence. The algorithmic problem of satisfiability concerns testing whether there exists a graph that models a given sentence.
Although both model checking and satisfiability are hard in general, several major algorithmic meta-theorems show that properties expressed in this way can be tested efficiently for important classes of graphs. (Full article...)
Image 9
Convergence of a convex curve to a circle under the curve-shortening flow. Inner curves (lighter color) are flowed versions of the outer curves. Time steps between curves are not uniform.

In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution.

As the points of any smooth simple closed curve move in this way, the curve remains simple and smooth. It loses area at a constant rate, and its perimeter decreases as quickly as possible for any continuous curve evolution. If the curve is non-convex, its total absolute curvature decreases monotonically, until it becomes convex. Once convex, the isoperimetric ratio of the curve decreases as the curve converges to a circular shape, before collapsing to a singularity. If two disjoint simple smooth closed curves evolve, they remain disjoint until one of them collapses to a point. (Full article...)
Image 10
As the degree of the Taylor polynomial rises, it approaches the correct function. This image shows $sin x$ and its Taylor approximations by polynomials of degree 1, 3, 5, 7, 9, 11, and 13 at $x = 0$ .

In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century.

The partial sum formed by the first $n + 1$ terms of a Taylor series is a polynomial of degree $n$ that is called the $n$ th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as $n$ increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of the infinite sequence of the Taylor polynomials. A function may differ from the sum of its Taylor series, even if its Taylor series is convergent. A function is analytic at a point $x$ if it is equal to the sum of its Taylor series in some open interval (or open disk in the complex plane) containing $x$ . This implies that the function is analytic at every point of the interval (or disk). (Full article...)
Image 11
A double bubble. Note that the surface separating the small lower bubble from the large bubble bulges into the large bubble.

In the mathematical theory of minimal surfaces, the double bubble theorem states that the shape that encloses and separates two given volumes and has the minimum possible surface area is a standard double bubble: three spherical surfaces meeting at angles of 120° on a common circle. The double bubble theorem was formulated and thought to be true in the 19th century, and became a "serious focus of research" by 1989, but was not proven until 2002.

The proof combines multiple ingredients. Compactness of rectifiable currents (a generalized definition of surfaces) shows that a solution exists. A symmetry argument proves that the solution must be a surface of revolution, and it can be further restricted to having a bounded number of smooth pieces. Jean Taylor's proof of Plateau's laws describes how these pieces must be shaped and connected to each other, and a final case analysis shows that, among surfaces of revolution connected in this way, only the standard double bubble has locally-minimal area. (Full article...)
Image 12
In geometry, the Dehn invariant is a value used to determine whether one polyhedron can be cut into pieces and reassembled ("dissected") into another, and whether a polyhedron or its dissections can tile space. It is named after Max Dehn, who used it to solve Hilbert's third problem by proving that certain polyhedra with equal volume cannot be dissected into each other.

Two polyhedra have a dissection into polyhedral pieces that can be reassembled into either one, if and only if their volumes and Dehn invariants are equal. Having Dehn invariant zero is a necessary (but not sufficient) condition for being a space-filling polyhedron, and a polyhedron can be cut up and reassembled into a space-filling polyhedron if and only if its Dehn invariant is zero. The Dehn invariant of a self-intersection-free flexible polyhedron is invariant as it flexes. Dehn invariants are also an invariant for dissection in higher dimensions, and (with volume) a complete invariant in four dimensions. (Full article...)

More good articles

Did you know (auto-generated) – load new batch

... that in 1967 two mathematicians published PhD dissertations independently disproving the same thirteen-year-old conjecture?
... that Kit Nascimento, a spokesperson for the government of Guyana during the aftermath of Jonestown, disagrees with current proposals to open the former Jonestown site as a tourist attraction?
... that people in Madagascar perform algebra on tree seeds in order to tell the future?
... that the discovery of Descartes' theorem in geometry came from a too-difficult mathematics problem posed to a princess?
... that the word algebra is derived from an Arabic term for the surgical treatment of bonesetting?
... that ten-sided gaming dice have kite-shaped faces?
... that despite published scholarship to the contrary, Andrew Planta neither received a doctorate nor taught mathematics at Erlangen?
... that in the aftermath of the American Civil War, the only Black-led organization providing teachers to formerly enslaved people was the African Civilization Society?

edit

More did you know – view different entries

Did you know...

...that every natural number can be written as the sum of four squares?
...that the largest known prime number is nearly 41 million digits long?
...that the set of rational numbers is equal in size to the set of integers; that is, they can be put in one-to-one correspondence?
...that there are precisely six convex regular polytopes in four dimensions? These are analogs of the five Platonic solids known to the ancient Greeks.
...that it is unknown whether π and e are algebraically independent?
...that a nonconvex polygon with three convex vertices is called a pseudotriangle?
...that it is possible for a three-dimensional figure to have a finite volume but infinite surface area, such as Gabriel's Horn?

More did you know facts

Showing 7 items out of 75

edit

Selected article – show another

Image credit: User:Fropuff

Knot theory is the branch of topology that studies mathematical knots, which are defined as embeddings of a circle S¹ in 3-dimensional Euclidean space, R³. This is basically equivalent to a conventional knotted string with the ends of the string joined together to prevent it from becoming undone. Two mathematical knots are considered equivalent if one can be transformed into the other via continuous deformations (known as ambient isotopies); these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.

Knots can be described in various ways, but the most common method is by planar diagrams (known as knot projections or knot diagrams). Given a method of description, a knot will have many descriptions, e.g., many diagrams, representing it. A fundamental problem in knot theory is determining when two descriptions represent the same knot. One way of distinguishing knots is by using a knot invariant, a "quantity" which remains the same even with different descriptions of a knot.

Research in knot theory began with the creation of knot tables and the systematic tabulation of knots. While tabulation remains an important task, today's researchers have a wide variety of backgrounds and goals. Classical knot theory, as initiated by Max Dehn, J. W. Alexander, and others, is primarily concerned with the knot group and invariants from homology theory such as the Alexander polynomial.

The discovery of the Jones polynomial by Vaughan Jones in 1984, and subsequent contributions from Edward Witten, Maxim Kontsevich, and others, revealed deep connections between knot theory and mathematical methods in statistical mechanics and quantum field theory. A plethora of knot invariants have been invented since then, utilizing sophisticated tools as quantum groups and Floer homology. (Full article...)

View all selected articles

edit

Subcategories

Full category tree. Select [►] to view subcategories.

More mathematics categories

edit

Topics in mathematics

General

Foundations

Number theory

Discrete mathematics

Algebra

Analysis

Geometry and topology

Applied mathematics

edit

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z