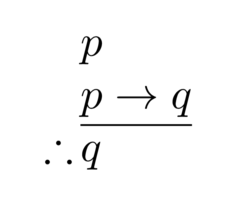Portal:Mathematics

---

The Mathematics Portal

Isaac Newton

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Featured articles –

  Featured articles are displayed here, which represent some of the best content on English Wikipedia.

---

• 
  
  

  

  Kaczynski after his arrest in 1996

  
  Theodore John Kaczynski (/kəˈzɪnski/ ^ⓘ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ ^ⓘ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. A mathematics prodigy, he abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle and lone wolf terrorism campaign.
  
  Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored a roughly 35,000-word manifesto and social critique called Industrial Society and Its Future which opposes all forms of technology, rejects leftism and fascism, advocates cultural primitivism, and ultimately suggests violent revolution. (Full article...)
• 

  

  Plots of logarithm functions, with three commonly used bases. The special points log_b b = 1 are indicated by dotted lines, and all curves intersect in log_b 1 = 0.

  
  
  In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the 3rd power: 1000 = 10³ = 10 × 10 × 10. More generally, if x = b^y, then y is the logarithm of x to base b, written log_b x, so log₁₀ 1000 = 3. As a single-variable function, the logarithm to base b is the inverse of exponentiation with base b.
  
  The logarithm base 10 is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number e ≈ 2.718 as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base 2 and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written log x. (Full article...)
• 

  

  The weighing pans of this balance scale contain zero objects, divided into two equal groups.

  
  In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
  
  Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
• 
  
  

  

  Noether c. 1900–1910

  
  Amalie Emmy Noether (23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's first and second theorems, which are fundamental in mathematical physics. Noether was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
  
  Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations, but instead studied mathematics at the University of Erlangen–Nuremberg, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
• 
  
  

  

  Portrait by August Köhler, c. 1910, after 1620 original

  
  Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.
  
  Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
  Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
• 

  

  
  Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
  
  Feynman developed a pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams and is widely used. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
• 
  
  

  

  Hilary Putnam

  
  The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.
  
  Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
• 

  

  
  Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American mechanical engineer and scientist who made fundamental theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.
  
  In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)
• 

  

  Logic studies valid forms of inference like modus ponens.

  
  
  Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.
  
  Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work." Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
• 
  
  

  

  A stamp of Zhang Heng issued by China Post in 1955

  
  Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.
  
  Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)
• 
  
  

  

  Elementary algebra studies which values solve equations formed using arithmetical operations.

  
  Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.
  
  Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
• 

  

  
  Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.
  
  Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...)
• 

  

  Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).

  
  
  In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
  It is an example of an algorithm, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.
  
  The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)
• 

  

  Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

  
  
  In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).
  
  In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution uses methods not limited to straightedge and compass constructions. François Viète found a straightedge and compass solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
• 

  

  The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group S̃₃

  
  The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.
  
  A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)

Selected image –

animation of dots of varying heights being sorted by height using the quicksort algorithm

Quicksort

Credit: RolandH

Quicksort (also known as the partition-exchange sort) is an efficient sorting algorithm that works for items of any type for which a total order (i.e., "≤") relation is defined. This animation shows how the algorithm partitions the input array (here a random permutation of the numbers 1 through 33) into two smaller arrays based on a selected pivot element (bar marked in red, here always chosen to be the last element in the array under consideration), by swapping elements between the two sub-arrays so that those in the first (on the left) end up all smaller than the pivot element's value (horizontal blue line) and those in the second (on the right) all larger. The pivot element is then moved to a position between the two sub-arrays; at this point, the pivot element is in its final position and will never be moved again. The algorithm then proceeds to recursively apply the same procedure to each of the smaller arrays, partitioning and rearranging the elements until there are no sub-arrays longer than one element left to process. (As can be seen in the animation, the algorithm actually sorts all left-hand sub-arrays first, and then starts to process the right-hand sub-arrays.) First developed by Tony Hoare in 1959, quicksort is still a commonly used algorithm for sorting in computer applications. On the average, it requires O(n log n) comparisons to sort n items, which compares favorably to other popular sorting methods, including merge sort and heapsort. Unfortunately, on rare occasions (including cases where the input is already sorted or contains items that are all equal) quicksort requires a worst-case O(n²) comparisons, while the other two methods remain O(n log n) in their worst cases. Still, when implemented well, quicksort can be about two or three times faster than its main competitors. Unlike merge sort, the standard implementation of quicksort does not preserve the order of equal input items (it is not stable), although stable versions of the algorithm do exist at the expense of requiring O(n) additional storage space. Other variations are based on different ways of choosing the pivot element (for example, choosing a random element instead of always using the last one), using more than one pivot, switching to an insertion sort when the sub-arrays have shrunk to a sufficiently small length, and using a three-way partitioning scheme (grouping items into those smaller, larger, and equal to the pivot—a modification that can turn the worst-case scenario of all-equal input values into the best case). Because of the algorithm's "divide and conquer" approach, parts of it can be done in parallel (in particular, the processing of the left and right sub-arrays can be done simultaneously). However, other sorting algorithms (including merge sort) experience much greater speed increases when performed in parallel.

Good articles –

  These are Good articles, which meet a core set of high editorial standards.

---

• 

  

  A double bubble. Note that the surface separating the small lower bubble from the large bubble bulges into the large bubble.

  
  In the mathematical theory of minimal surfaces, the double bubble theorem states that the shape that encloses and separates two given volumes and has the minimum possible surface area is a standard double bubble: three spherical surfaces meeting at angles of 120° on a common circle. The double bubble theorem was formulated and thought to be true in the 19th century, and became a "serious focus of research" by 1989, but was not proven until 2002.
  
  The proof combines multiple ingredients. Compactness of rectifiable currents (a generalized definition of surfaces) shows that a solution exists. A symmetry argument proves that the solution must be a surface of revolution, and it can be further restricted to having a bounded number of smooth pieces. Jean Taylor's proof of Plateau's laws describes how these pieces must be shaped and connected to each other, and a final case analysis shows that, among surfaces of revolution connected in this way, only the standard double bubble has locally-minimal area. (Full article...)
• 

  

  Schwarz lantern on display in the German Museum of Technology, Berlin

  
  
  In mathematics, the Schwarz lantern is a polyhedral approximation to a cylinder, used as a pathological example of the difficulty of defining the area of a smooth (curved) surface as the limit of the areas of polyhedra. It is formed by stacked rings of isosceles triangles, arranged within each ring in the same pattern as an antiprism. The resulting shape can be folded from paper, and is named after mathematician Hermann Schwarz and for its resemblance to a cylindrical paper lantern. It is also known as Schwarz's boot, Schwarz's polyhedron, or the Chinese lantern.
  
  As Schwarz showed, for the surface area of a polyhedron to converge to the surface area of a curved surface, it is not sufficient to simply increase the number of rings and the number of isosceles triangles per ring. Depending on the relation of the number of rings to the number of triangles per ring, the area of the lantern can converge to the area of the cylinder, to a limit arbitrarily larger than the area of the cylinder, or to infinity—in other words, the area can diverge. The Schwarz lantern demonstrates that sampling a curved surface by close-together points and connecting them by small triangles is inadequate to ensure an accurate approximation of area, in contrast to the accurate approximation of arc length by inscribed polygonal chains. (Full article...)
• 

  

  A Halin graph

  
  In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle.
  The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross (this is called a planar embedding), and the cycle
  connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.
  
  Halin graphs are named after German mathematician Rudolf Halin, who studied them in 1971.
  The cubic Halin graphs – the ones in which each vertex touches exactly three edges – had already been studied over a century earlier by Kirkman.
  Halin graphs are polyhedral graphs, meaning that every Halin graph can be used to form the vertices and edges of a convex polyhedron, and the polyhedra formed from them have been called roofless polyhedra or domes. (Full article...)
• 

  

  Wave functions of the electron in a hydrogen atom at different energy levels. Quantum mechanics cannot predict the exact location of a particle in space, only the probability of finding it at different locations. The brighter areas represent a higher probability of finding the electron.

  
  Quantum mechanics is the fundamental physical theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science.
  
  Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. (Full article...)
• 

  

  Which point on the surface of the spherical mirror can reflect a ray of light from the candle to the observer's eye?

  
  Alhazen's problem is a mathematical problem in optics concerning reflection in a spherical mirror. It asks for the point in the mirror where one given point reflects to another.
  The special case of a concave spherical mirror is also known as Alhazen's billiard problem, as it can be formulated equivalently as constructing a reflected path from one billiard ball to another on a circular billiard table. Other equivalent formulations ask for the shortest path from one point to the other that touches the circle, or for an ellipse that is tangent to the circle and has the given points as its foci.
  
  Although special cases of this problem were studied by Ptolemy in the 2nd century CE, it is named for the 11th-century Arab mathematician Alhazen (Hasan Ibn al-Haytham), who formulated it more generally and presented a solution in his Book of Optics. It has no straightedge and compass construction; instead, al-Haytham and others including Christiaan Huygens found solutions involving the intersection of conic sections. According to Roberto Marcolongo, Leonardo da Vinci invented a mechanical device to solve the problem. Later mathematicians, starting with Jack M. Elkin in 1965, solved the problem algebraically as the solution to a quartic equation, and used this equation to prove the impossibility of solving the problem with straightedge and compass. (Full article...)
• 

  

  In this graph, the widest path from Maldon to Feering has bandwidth 29, and passes through Clacton, Tiptree, Harwich, and Blaxhall.

  
  In graph algorithms, the widest path problem is the problem of finding a path between two designated vertices in a weighted graph, maximizing the weight of the minimum-weight edge in the path. The widest path problem is also known as the maximum capacity path problem. It is possible to adapt most shortest path algorithms to compute widest paths, by modifying them to use the bottleneck distance instead of path length. However, in many cases even faster algorithms are possible.
  
  For instance, in a graph that represents connections between routers in the Internet, where the weight of an edge represents the bandwidth of a connection between two routers, the widest path problem is the problem of finding an end-to-end path between two Internet nodes that has the maximum possible bandwidth. The smallest edge weight on this path is known as the capacity or bandwidth of the path. As well as its applications in network routing, the widest path problem is also an important component of the Schulze method for deciding the winner of a multiway election, and has been applied to digital compositing, metabolic pathway analysis, and the computation of maximum flows. (Full article...)
• 
  Basic Math is an educational video game programmed by Gary Palmer and published by Atari, Inc. for the Atari Video Computer System. The game features a series of ten arithmetic problems involving addition, subtraction, multiplication, or division. The player can edit different gameplay modes to alter how the numbers in the problem are chosen, or if their questions are timed. The game was released in September 1977 as one of the earliest releases for the Atari VCS.
  
  The game is the only known game developed for the VCS by Palmer, who initially worked at Atari creating debugging stations for game developers, and later assisted with work on the Atari 400/800 line of computers. It was the first educational video game for the VCS, with other companies also releasing arithmetic-themed cartridges in the same year for the Fairchild Channel F and RCA Studio II. Both contemporary and retrospective reviews were generally unenthused by the game, with common criticism being that it had poor quality graphics and was not appealing in terms of gameplay or control. (Full article...)
• 
  
  

  

  Huygens by Caspar Netscher (1671), Museum Boerhaave, Leiden

  
  Christiaan Huygens, Lord of Zeelhem, FRS (/ˈhaɪɡənz/ HY-gənz, US also /ˈhɔɪɡənz/ HOY-gənz; Dutch: [ˈkrɪstijaːn ˈɦœyɣə(n)s] ^ⓘ; also spelled Huyghens; Latin: Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution. In physics, Huygens made seminal contributions to optics and mechanics, while as an astronomer he studied the rings of Saturn and discovered its largest moon, Titan. As an engineer and inventor, he improved the design of telescopes and invented the pendulum clock, the most accurate timekeeper for almost 300 years. A talented mathematician and physicist, his works contain the first idealization of a physical problem by a set of mathematical parameters, and the first mathematical and mechanistic explanation of an unobservable physical phenomenon.
  
  Huygens first identified the correct laws of elastic collision in his work De Motu Corporum ex Percussione, completed in 1656 but published posthumously in 1703. In 1659, Huygens derived geometrically the formula in classical mechanics for the centrifugal force in his work De vi Centrifuga, a decade before Isaac Newton. In optics, he is best known for his wave theory of light, which he described in his Traité de la Lumière (1690). His theory of light was initially rejected in favour of Newton's corpuscular theory of light, until Augustin-Jean Fresnel adapted Huygens's principle to give a complete explanation of the rectilinear propagation and diffraction effects of light in 1821. Today this principle is known as the Huygens–Fresnel principle. (Full article...)
• 
  
  

  

  8x8 Rook's graph

  
  In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and there is an edge between any two squares sharing a row (rank) or column (file), the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape. Although rook's graphs have only minor significance in chess lore, they are more important in the abstract mathematics of graphs through their alternative constructions: rook's graphs are the Cartesian product of two complete graphs, and are the line graphs of complete bipartite graphs. The square rook's graphs constitute the two-dimensional Hamming graphs.
  
  Rook's graphs are highly symmetric, having symmetries taking every vertex to every other vertex. In rook's graphs defined from square chessboards, more strongly, every two edges are symmetric, and every pair of vertices is symmetric to every other pair at the same distance in moves (making the graph distance-transitive). For rectangular chessboards whose width and height are relatively prime, the rook's graphs are circulant graphs. With one exception, the rook's graphs can be distinguished from all other graphs using only two properties: the numbers of triangles each edge belongs to, and the existence of a unique 4-cycle connecting each nonadjacent pair of vertices. (Full article...)
• 

  

  
  Jessen's icosahedron, sometimes called Jessen's orthogonal icosahedron, is a non-convex polyhedron with the same numbers of vertices, edges, and faces as the regular icosahedron. It is named for Børge Jessen, who studied it in 1967. In 1971, a family of nonconvex polyhedra including this shape was independently discovered and studied by Adrien Douady under the name six-beaked shaddock; later authors have applied variants of this name more specifically to Jessen's icosahedron.
  
  The faces of Jessen's icosahedron meet only in right angles, even though it has no orientation where they are all parallel to the coordinate planes. It is a "shaky polyhedron", meaning that (like a flexible polyhedron) it is not infinitesimally rigid. Outlining the edges of this polyhedron with struts and cables produces a widely used tensegrity structure, also called the six-bar tensegrity, tensegrity icosahedron, or expanded octahedron. (Full article...)
• 
  
  

  

  Roman copy (in marble) of a Greek bronze bust of Aristotle by Lysippos (c. 330 BC), with modern alabaster mantle

  
  Aristotle (Attic Greek: Ἀριστοτέλης, romanized: Aristotélēs; 384–322 BC) was an Ancient Greek philosopher and polymath. His writings cover a broad range of subjects spanning the natural sciences, philosophy, linguistics, economics, politics, psychology, and the arts. As the founder of the Peripatetic school of philosophy in the Lyceum in Athens, he began the wider Aristotelian tradition that followed, which set the groundwork for the development of modern science.
  
  Little is known about Aristotle's life. He was born in the city of Stagira in northern Greece during the Classical period. His father, Nicomachus, died when Aristotle was a child, and he was brought up by a guardian. At around eighteen years old, he joined Plato's Academy in Athens and remained there until the age of thirty seven (c. 347 BC). Shortly after Plato died, Aristotle left Athens and, at the request of Philip II of Macedon, tutored his son Alexander the Great beginning in 343 BC. He established a library in the Lyceum, which helped him to produce many of his hundreds of books on papyrus scrolls. (Full article...)
• 
  
  

  

  Wigner in 1963

  
  Eugene Paul Wigner (Hungarian: Wigner Jenő Pál, pronounced [ˈviɡnɛr ˈjɛnøː ˈpaːl]; November 17, 1902 – January 1, 1995) was a Hungarian-American theoretical physicist who also contributed to mathematical physics. He received the Nobel Prize in Physics in 1963 "for his contributions to the theory of the atomic nucleus and the elementary particles, particularly through the discovery and application of fundamental symmetry principles".
  
  A graduate of the Technical Hochschule Berlin (now Technische Universität Berlin), Wigner worked as an assistant to Karl Weissenberg and Richard Becker at the Kaiser Wilhelm Institute in Berlin, and David Hilbert at the University of Göttingen. Wigner and Hermann Weyl were responsible for introducing group theory into physics, particularly the theory of symmetry in physics. Along the way he performed ground-breaking work in pure mathematics, in which he authored a number of mathematical theorems. In particular, Wigner's theorem is a cornerstone in the mathematical formulation of quantum mechanics. He is also known for his research into the structure of the atomic nucleus. In 1930, Princeton University recruited Wigner, along with John von Neumann, and he moved to the United States, where he obtained citizenship in 1937. (Full article...)

Did you know (auto-generated) –

• ... that the identity of Cleo, who provided online answers to complex mathematics problems without showing any work, was revealed over a decade later in 2025?
• ... that the role of the British Mobile Defence Corps was to carry out rescue work in the aftermath of a nuclear attack?
• ... that Fathimath Dheema Ali is the first Olympic qualifier from the Maldives?
• ... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
• ... that 17th-century mathematician Carlo Rinaldini studied gall-inducing insects, air convection, and the design of thermometers?
• ... that Hong Wang's latest paper claims to have resolved the Kakeya conjecture, described as "one of the most sought-after open problems in geometric measure theory", in three dimensions?
• ... that Hannah Fry used mathematics to compare Elizabeth II's Christmas messages with the lyrics of Snoop Dogg?
• ... that Latvian-Soviet artist Karlis Johansons exhibited a skeletal tensegrity form of the Schönhardt polyhedron seven years before Erich Schönhardt's 1928 paper on its mathematics?

More did you know –

Did you know...

• ...that in Floyd's algorithm for cycle detection, the tortoise and hare move at very different speeds, but always finish at the same spot?
• ...that in graph theory, a pseudoforest can contain trees and pseudotrees, but cannot contain any butterflies, diamonds, handcuffs, or bicycles?
• ...that it is not possible to configure two mutually inscribed quadrilaterals in the Euclidean plane, but the Möbius–Kantor graph describes a solution in the complex projective plane?
• ...that the six permutations of the vector (1,2,3) form a hexagon in 3D space, the 24 permutations of (1,2,3,4) form a truncated octahedron in four dimensions, and both are examples of permutohedra?
• ...that the Rule 184 cellular automaton can simultaneously model the behavior of cars moving in traffic, the accumulation of particles on a surface, and particle-antiparticle annihilation reactions?
• ...that a cyclic cellular automaton is a system of simple mathematical rules that can generate complex patterns mixing random chaos, blocks of color, and spirals?
• ...that a nonconvex polygon with three convex vertices is called a pseudotriangle?

Selected article –

Flowcharts are often used to represent algorithms Image credit: User:Booyabazooka

An algorithm is a procedure (a finite set of well-defined instructions) for accomplishing some task which, given an initial state, will terminate in a defined end-state. The computational complexity and efficient implementation of the algorithm are important in computing, and this depends on suitable data structures.

Informally, the concept of an algorithm is often illustrated by the example of a recipe, although many algorithms are much more complex; algorithms often have steps that repeat (iterate) or require decisions (such as logic or comparison). Algorithms can be composed to create more complex algorithms.

The concept of an algorithm originated as a means of recording procedures for solving mathematical problems such as finding the common divisor of two numbers or multiplying two numbers. The concept was formalized in 1936 through Alan Turing's Turing machines and Alonzo Church's lambda calculus, which in turn formed the foundation of computer science.

Most algorithms can be directly implemented by computer programs; any other algorithms can at least in theory be simulated by computer programs. In many programming languages, algorithms are implemented as functions or procedures. (Full article...)

View all selected articles

Subcategories

Algebra | Arithmetic | Analysis | Complex analysis | Applied mathematics | Calculus | Category theory | Chaos theory | Combinatorics | Dynamical systems | Fractals | Game theory | Geometry | Algebraic geometry | Graph theory | Group theory | Linear algebra | Mathematical logic | Model theory | Multi-dimensional geometry | Number theory | Numerical analysis | Optimization | Order theory | Probability and statistics | Set theory | Statistics | Topology | Algebraic topology | Trigonometry | Linear programming

---

Mathematics | History of mathematics | Mathematicians | Awards | Education | Literature | Notation | Organizations | Theorems | Proofs | Unsolved problems

Full category tree. Select [►] to view subcategories.

Mathematics

Mathematics by country

Fields of mathematics

Mathematics-related lists

Mathematicians

Women in mathematics

Works about mathematics

Mathematics and art

Bruhat family

Choquet family

Mathematical classification systems

Mathematical concepts

Mathematical constants

Mathematics and culture

Eponyms in mathematics

Mathematical examples

History of mathematics

Mathematics occupations

Mathematical notation

Outlines of mathematics and logic

Philosophy of mathematics

Mathematical projects

Mathematical proofs

Pseudomathematics

Set index articles on mathematics

Mathematical terminology

Mathematical theorems

Mathematical tools

Mathematics stubs

Topics in mathematics

General

• Mathematicians
• History of mathematics
• Philosophy of mathematics
• Mathematical notation
• Mathematical beauty
• Mathematics education
• Glossary of mathematical symbols

Foundations

• Foundations of mathematics
• Mathematical logic
  • Proof theory
    • Gödel's incompleteness theorems
  • Model theory
  • Recursion theory
• Set theory
  • Naive set theory
  • Axiomatic set theory
• Category theory
  • Topos theory

Number theory

• Number theory
• Algebraic number theory
• Analytic number theory
• Arithmetic
  • Fundamental theorem of arithmetic
• Numbers
  • Natural numbers
  • Prime numbers
  • Rational numbers
  • Algebraic numbers

Discrete mathematics

• Discrete mathematics
• Combinatorics
  • Combinatorial geometry
  • Coding theory
  • Combinatorial design
  • Enumerative combinatorics
  • Combinatorial optimization
• Graph theory
• Order theory
  • Lattice theory
• Digital Signal Processing
• Theoretical computer science
  • Computability theory
  • Complexity theory

Algebra

• Algebra
• Elementary algebra
• Abstract algebra
  • Group theory
  • Ring theory
  • Field theory
  • Commutative algebra
• Geometric algebra
• Linear algebra
  • Matrix theory
  • Multilinear algebra
• Universal algebra
• Fundamental theorem of algebra

Analysis

• Analysis
• Calculus
  • Fundamental theorem of calculus
  • Vector calculus
  • Geometric calculus
• Measure theory
• Real analysis
• Complex analysis
• Differential equations
  • Ordinary differential equations
  • Partial differential equations
• Integral equations
• Approximation theory
• Special functions
• Potential theory
• Harmonic analysis
  • Fourier analysis
• Functional analysis
• Operator theory

Geometry and topology

• Geometry
• Euclidean geometry
  • Trigonometry
• Analytic geometry
• Non-Euclidean geometry
• Affine geometry
• Projective geometry
• Convex geometry
• Discrete geometry
• Algebraic geometry
• Differential geometry
  • K theory
  • Gauge theory
  • Riemannian geometry
  • Lie groups
• Topology
  • General topology
  • Algebraic topology
  • Geometric topology
  • Differential topology

Applied mathematics

• Applied mathematics
• Mathematical modeling
• Mathematical physics
• Dynamical systems
  • Control theory
  • Calculus of variations
• Optimization
• Mathematical economics
  • Game theory
  • Mathematical finance
• Statistics
• Probability theory
  • Stochastic processes
• Numerical analysis
• Cryptography
• Information theory

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Related portals

WikiProjects

The Mathematics WikiProject is the center for mathematics-related editing on Wikipedia. Join the discussion on the project's talk page.

Project pages

• Participants
• Current activity
• Manual of style
• Conventions

Essays

• Advice on using Wikipedia for mathematics self-study
• Proofs

Subprojects

• PlanetMath Exchange (Talk)
• Graphics (Talk)
• Article assessment (Talk)

Related projects

Computer science | Cryptography | Game theory | Numbers | Physics | Science | Statistics

Things you can do

• Create a new article: List of requested articles
• Add a new image: Image requests
• Expand an article: Mathematics stubs
• Lend your expertise: Expert attention needed

In other Wikimedia projects

The following Wikimedia Foundation sister projects provide more on this subject:

• 

  Commons
  Free media repository

• 

  Wikibooks
  Free textbooks and manuals

• 

  Wikidata
  Free knowledge base

• 

  Wikinews
  Free-content news

• 

  Wikiquote
  Collection of quotations

• 

  Wikisource
  Free-content library

• 

  Wikiversity
  Free learning tools

• 

  Wiktionary
  Dictionary and thesaurus

More portals

Discover Wikipedia using portals

• 

  List of all portals
• 
  The arts portal
• 
  Biography portal
• 
  Current events portal
• 
  Geography portal
• 
  History portal
• 
  Mathematics portal
• 
  Science portal
• 
  Society portal
• 
  Technology portal

• 

  Random portal

• 

  WikiProject Portals